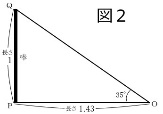
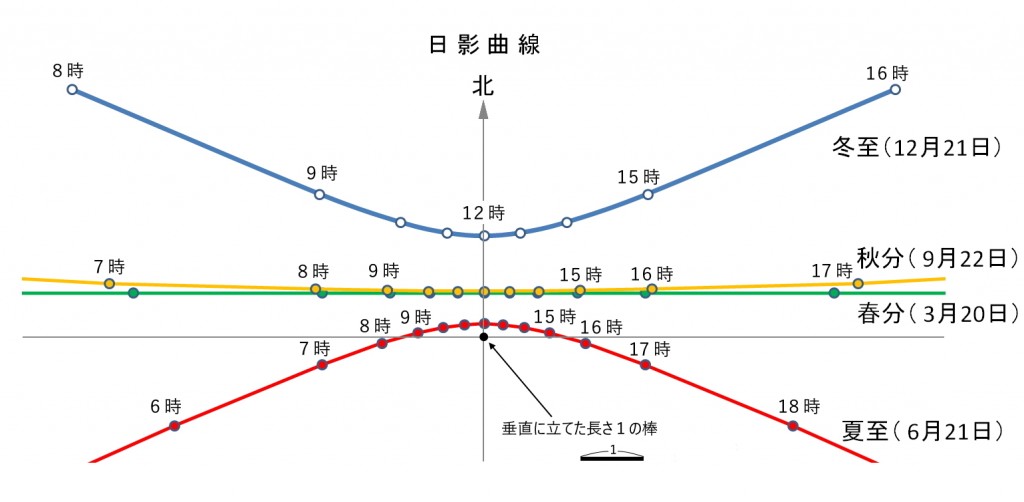
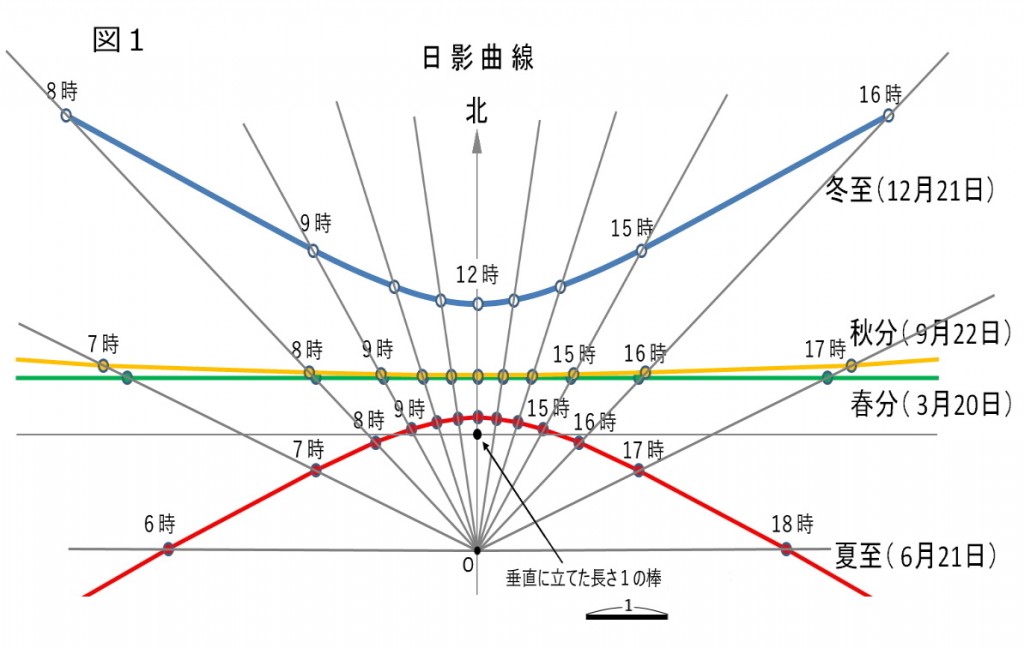
図１は前回に説明した日影曲線ですが、図中の4つの季節の日影曲線上の同じ時刻の点をつなぐと一本の直線になり、それらの直線がなんと一点（点Ｏと名付ける）で交わります。この点Ｏは日影曲線を描くために立てた棒の位置（点Ｐと名付ける）から棒の長さの1.43倍の距離にあります。棒の先端をＱ点として、棒と点Ｏでできる直角三角形ＰＯＱを描くと図２のようになり、頂点Ｏの角度は35°で日影曲線を描くとき使った豊中の緯度35°と一致しています。と言うことは直線ＯＱはＱの方に延長していくと北極星に当たるということで、また直線ＯＱは地軸に平行ということです。

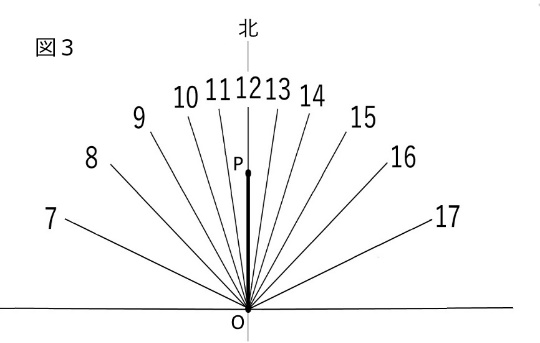
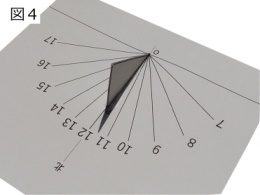
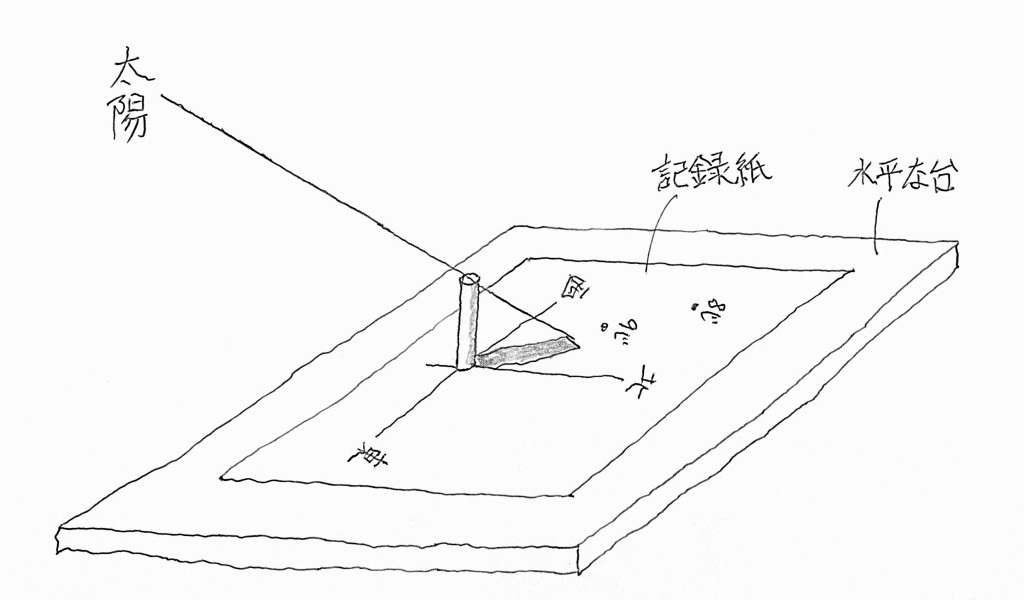
では、いよいよ日時計を作りましょう。下の図３は上の日影曲線にある同時刻の点をつないだ直線群だけにしたもので、日時計の文字盤になります。この文字盤に図２の直角三角形の板を点Ｏが一致するように文字盤の南北の線上に立てれば完成（図４）です。

ここでは豊中（北緯35°付近）で使うことを前提にしていますので豊中から大きく北や南に離れると不正確になります。

また、文字盤に取り付ける三角形については、時刻を読み取るのは直線ＯＱの影を利用するので、極端に言えば三角形の板ではなく水平面と35°をなすまっすぐで適当な長さの棒で良いのです。このことを利用して自分なりの日時計を作ることもできます。

私たちが日常使っている「時間」は太陽の動きから決められているので、地面に垂直に立てられた棒の影の位置から今の時刻を知ることができます。そこで、板に垂直に棒を立てその板を日当たりのよいところに水平に置いて、太陽による棒の先端の影を朝から夕方にかけて板に記録していくと曲線ができて、この曲線を「日影曲線」といいます。この曲線上の７時，８時・・・・の正時刻の点を記録しておくと日時計ができます。

棒の影を観察

太陽の１日の動きは中学３年理科の地学分野で勉強します。それによると太陽の動きは年間を通じて一定ではなく、春（春分の日）には真東から出て真西に沈みます。その日から少しずつ北に移動して夏至の日には東から約29度北に寄ったところから出て、真西から約29度北に寄ったところに沈みます。夏至を過ぎると南に移動を始め秋（秋分の日）には真東から出て真西に沈みます。秋分の日のあとさらに南に移動して冬至の日には東から約29度南に寄ったところから出て、沈む位置は真西から約29度南に寄ったところになります。冬至を過ぎると北に移動を始め春（春分の日）に戻ります。１年の周期で変化するわけです。この変化は地球の自転軸が公転面に垂直な方向から23.4°傾いていることによって生じており、日本（地球の中緯度地域）に四季をもたらしています。さらに観測する緯度によっても太陽の位置（高度）が変わるので「日影曲線」は日時と場所によって変わります。

ここで、場所は豊中（北緯35°）として春分・夏至・秋分・冬至それぞれの日の日影曲線を紹介しましょう。ただし、この曲線は実際に測定して得たものではなく、私がエクセルを利用して計算によってシミュレートしたものです。

日影曲線

次回はこの曲線を利用して日時計を作製したいと思います。